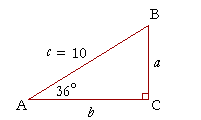How do you use the Pythagorean Theorem to determine if the

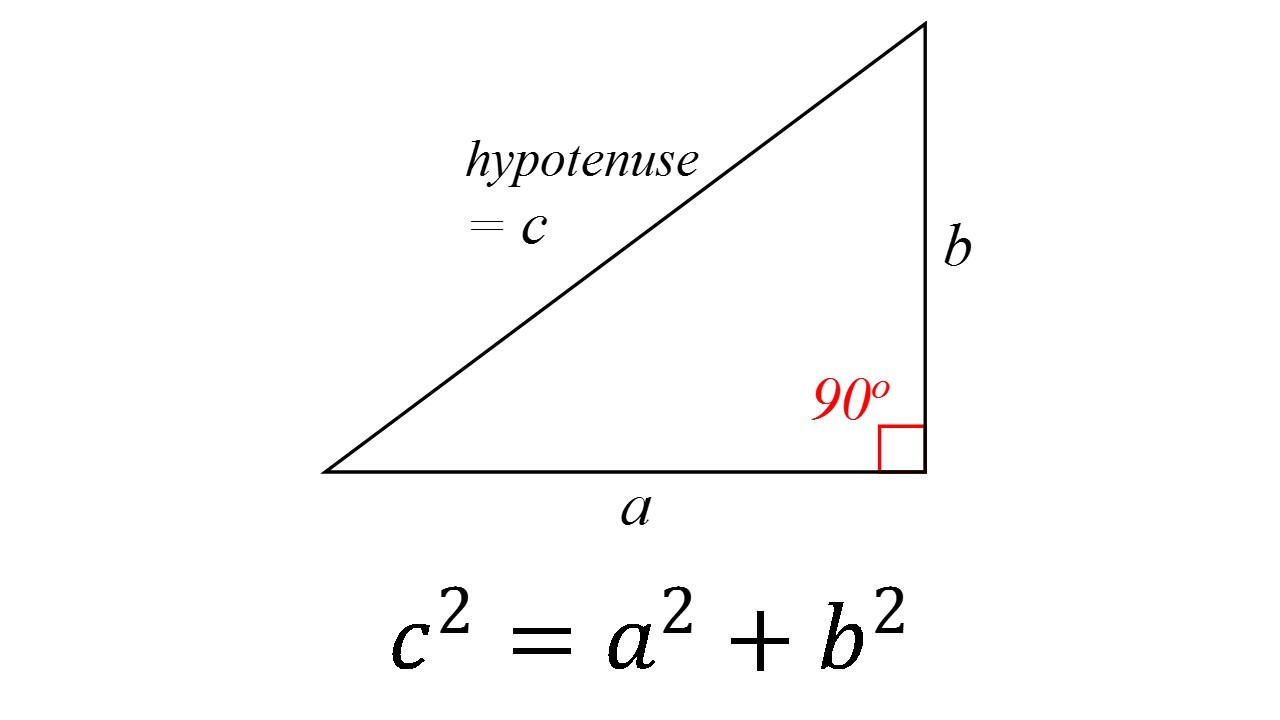
c^2 != a^2 + b^2, therefore, this cannot be a right triangle. The Pythagorean Theorem applies to right angle triangles, where the sides a and b are those which intersect at right angle. The third side, the hypotenuse, is then c To test whether the given lengths of sides create a right triangle, we need to substitute them into the Pythagorean Theorem - if it works out then it is a right angle triangle: c^2 = a^2 + b^2 15^2 != 5^2+10^2 225 != 25+100 225 != 125 In reality, if a=5 and b=10 then c would have to be c^2 = 125 c =sqrt(125) = 5sqrt(5)~= 11.2 which is smaller than the proposed value in the question. Therefore, this cannot be a right triangle.

Pythagorean Theorem - Math Steps, Examples & Questions

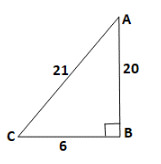
How do you use the Pythagorean theorem to determine if the following three numbers could represent the measures of the sides of a right triangle: 20, 6, 21?

Use Pythagorean Theorem to find Perimeter

How To Verify A Triangle Is A Right Triangle Using The Pythagorean Theorem Explained

Identifying right-angled triangles - Pythagoras' theorem - CCEA - GCSE Maths Revision - CCEA - BBC Bitesize

Pythagorean Theorem Calculator - Steps to Solve - Inch Calculator

Pythagorean Theorem Calculator

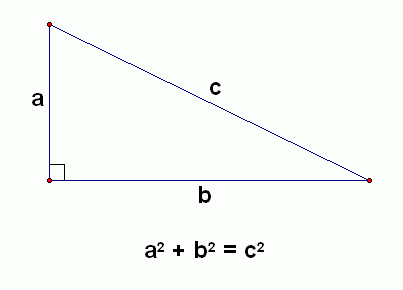
The Pythagorean Theorem - Trigonometry

How do you use the Pythagorean Theorem to determine if the following three numbers could represent the measures of the sides of a right triangle: 6, 8, 10?

Can you use the Pythagorean theorem to find an angle? - Quora

How to Use Pythagorean Theorem Converse: Is This a Right Triangle? - Effortless Math: We Help Students Learn to LOVE Mathematics

URGENT. i wasn't at school all week due to the flu and I really need help on these Pythagorean theorem

Apply the Pythagorean theorem. Find whether the given triangle has a right angle.

Use the Pythagorean Theorem to determine the missing side of the right triangle where the two sides are of lengths 13 and 8 units. A) sqrt(233) units B) sqrt(105) units C) sqrt(21)